Reduce NuGet restore times by using ‘Nearest Wins’
- Open Source Software
Written by Marcin Krystianc, Open-Source Software Developer
In one of our previous NuGet posts about central package version management, we outlined that for some solutions the restore operation was slow.
We decided to delve a little deeper and see whether optimising NuGet could make the restore function go faster.
How it started
Our investigation started when one of our teams wanted to move their solution from .NET Framework to .NET Core. To their surprise, updating the TargetFramework made the NuGet restore time go through the roof – it shot up from a minute and a half to 16 minutes.
As our original solution is sensitive to our business, we can’t share it, but what we can do is share some representative examples to demonstrate how we moved forward.
For our examples below, we used SanitisedNet471 and SanitisedNetCoreApp3.1, which are both available publicly. They suffer from the same performance problem, only on a slightly smaller scale. In their case, the restore time jumps from 14 to 42 seconds.
In our company, we care a lot about the productivity of developers. So keeping our CI cycles short is a priority. After reporting the issue to the NuGet maintainers, we continued to analyse the problem to find its root cause.
Observations and questions
When running NuGet.exe under a profiler, we were easily able to narrow the problem to the WalkDependenciesAsync method.
For the .NET framework solution it was responsible for 40% of the restore time, and for the .NET core variant it was a big 75%.
Another discovery was that the number of calls of the inner CreateGraphNode method went up to 25 million from 2 million.
While these findings are interesting in themselves, they also led to further questions within our team:
- Why did the number of graph nodes created internally increase significantly when we switched the target framework to .NET Core?
- Given that the solutions we are talking about are manageable in size (340 projects, 4,000 project references, 90 unique NuGet packages and 600 package references), why is the number of internal graph nodes counted in millions?
Theories and investigation
We had enough information at this point to suspect that the problem might be caused by exponential complexity hiding somewhere in the restore algorithm. A closer look at the code with the aid of a debugger confirmed our theory.
It turns out that the way in which NuGet walks the dependency graph is not very scalable. It works well only up to a certain solution size whereas for larger solutions its exponential nature starts to dominate.
To better explain the problem we’ve prepared a synthetic solution called RestoreBomb; its structure is shown on the diagram below:
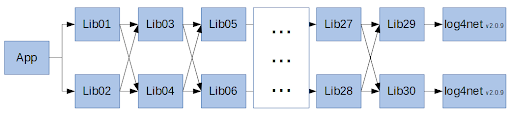
The restore algorithm walks the dependency graph and converts it into a tree. Our example is designed in such a way that it immediately shows why conversion to a tree is a problem:
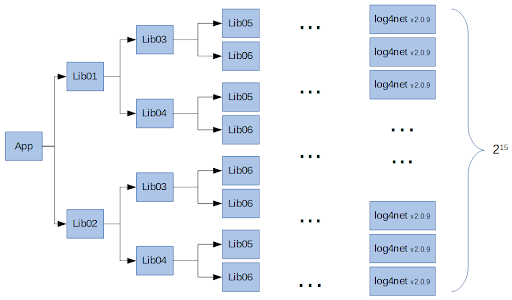
We can clearly see that for each depth-level of our dependency graph, the number of nodes needed to represent a tree is doubled. Since the depth of our dependency graph is 15, the total number of log4net nodes in the tree equals 215 (32,768).
But the increase doesn’t end there: log4net itself has its own rich dependency graph, so the total number of nodes in the final tree is counted in millions.
Getting closer: The Nearest Wins algorithm
Why exactly does NuGet need to expand a dependency graph into a tree? It is because of the dependency resolution rule that is called Nearest Wins.
In principle, it means that in the case of multiple dependencies on the same package, but with different versions, the “nearest” dependency has a higher priority than the rest.
However despite the name and the documentation, our analysis shows priority is not really about distance from the root project, instead what matters more is the relationship between nodes and their direct and transitive dependencies.
There are two conditions that need to be true for a dependency to be determined as “nearest”. Firstly, it needs to be a direct dependency of node X. Secondly, the other dependency must sit within the subtree of node X.
If the dependency is determined as “nearest” then it is preferred over other dependencies with the same name but a different version.
In cases where the “Nearest Wins” rule doesn’t apply, a dependency with a higher version is simply preferred over dependencies with a lower version (e.g. `v2.0.0` is preferred over `v1.0.0`).
For a concrete example let’s look at the diagram below:
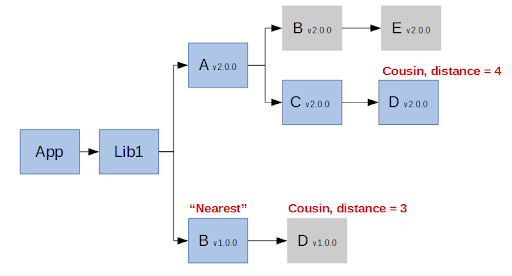
Package `B v1.0.0` is considered “nearest” because both `B v1.0.0` and `B v2.0.0` are in the subtree of `Lib1` and `B v1.0.0` is a direct dependency of `Lib1`. Package `B v1.0.0` is preferred over `B v2.0.0`in this case.
On the contrary, package `D v1.0.0` is closer to the root project than the `D v2.0.0`, but it is not considered “nearest” because the `D v1.0.0` is a direct dependency of `B v1.0.0`, but `D v2.0.0` is not in the subtree of `B v1.0.0`. In this case package `D v2.0.0` is chosen.
The “Nearest Wins” rule is a little bit complicated but there is a reason for that; it lets us be explicit about our intentions when an engineer wants to downgrade a version of the NuGet package.
For example, `Lib1` asks explicitly for a lower version of the `B` package, but it doesn’t cause an accidental downgrade of package `D` at the same time.
Conclusion
In this post, we’ve shown why NuGet can be very slow if the solution reaches a certain size.
For small and shallow dependency graphs this problem is somewhat negligible. However, for larger and deeper dependency graphs, the exponential nature of the restore algorithm becomes a major bottleneck. In extreme cases, it can even make the restore operation impractical, which is what we have encountered ourselves.
The good news is that we believe it is possible to reimplement NuGet’s restore algorithm in a way that would be backward compatible, and at the same time would be much more efficient. The key idea would be to avoid converting the input graph into a dependency tree, and apply the “Nearest Wins” rule directly on the input graph itself. It is a concept that we are going to explore further in another post, so stay tuned.
