G-Research were headline sponsors at NeurIPS 2022, in New Orleans.
ML is a fast-evolving discipline; attending conferences like NeurIPS and keeping up-to-date with the latest developments is key to the success of our quantitative researchers and machine learning engineers.
Our NeurIPS 2022 paper review series gives you the opportunity to hear about the research and papers that our quants and ML engineers found most interesting from the conference.
Here, Vuk R, Quantitative Researcher at G-Research, discusses two papers from NeurIPS:
- Sheaf Attention Networks
- The Union of Manifolds Hypothesis
Sheaf Attention Networks
Federico Barbero, Cristian Bodnar, Haitz Sáez-de-Ocáriz-Borde, Pietro Liò
Increasingly popular Graph Neural Networks (GNNs) often have problems with feature over-smoothing and datasets where data lives on heterophilic graphs.
Sheaf Neural Networks (SNNs) tackle these issues by endowing graphs with topological structures called cellular sheaves. The authors of this paper further enhance the reputation of SNNs by introducing attention and highlighting how Sheaf Attention Networks (SheafATs) can beat Graph Attention Networks (GATs) on a variety of benchmarks.
The most interesting element of the paper is the synergy between algebraic topology and deep learning. The authors use the idea of sheaves and combine it with popular attention mechanics.
They first construct the sheaf diffusion equation that describes evolution of a feature in time, and discretise it to get the equation for the SheafAN layer. Additionally, they consider another solution that leads to Res-SheafANs, a class of networks that features residual connections, which serve as low and high pass filters.
Finally, they compare Res-SheafANs and SheafAN with various other popular GNN architectures. The two seem to perform similarly: consistently beating GATs and placing in top three architectures most of the time.
In one comparison, these networks have the issue of running out of memory before producing the result. Hopefully this will lead to further research into reducing the memory cost while keeping the expressivity of these models.
The Union of Manifolds Hypothesis
Bradley C.A. Brown, Anthony L. Caterini, Brendan Leigh Ross, Jesse C. Cresswell, Gabriel Loaiza-Ganem
The Manifold Hypothesis, which states that high-dimensional structured data often lives on a low-dimensional manifold, has been widely accepted within the deep learning community. However, the authors here propose a modification called The Union of Manifolds Hypothesis. This modification says that the data lives on a union of low-dimensional manifolds instead of on a single one, which allows for these manifolds to have varying dimensions across the dataset as there are no reasons for, for example, pictures of dogs and trees to live on the same smaller manifold, or even manifolds of the same dimension.
They naturally choose to divide data points based on classes and compute intrinsic dimension of a manifold corresponding to each class. To estimate the intrinsic dimension of a manifold they use the following estimator:
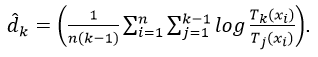
Here, ![]() is the Euclidean distance from i-th data point to its k-th (a hyperparameter) nearest neighbour, and n is the number of data points that are thought to live on that manifold.
is the Euclidean distance from i-th data point to its k-th (a hyperparameter) nearest neighbour, and n is the number of data points that are thought to live on that manifold.
To support the hypothesis, they evaluate the estimator on a number of image datasets. They find that the estimates are somewhat consistent for a range of values of k, and as well as that, the dimensions of these manifold vary significantly. Additionally, they find that instrinsic dimension is negatively correlated with the test accuracy (which intuitively says that higher dimensional data is harder to learn), and that weighting the examples in loss function by intrinsic dimension improves accuracy of ResNet-18 on CIFAR-100.

