This article is one of a series of paper reviews from our researchers and machine learning engineers – view more

Last month, G-Research were Diamond sponsors at ICML, hosted this year in Baltimore, US.
As well as having a stand and team in attendance, a number of our quantitative researchers and machine learning engineers attended as part of their ongoing learning and development.
We asked our quants and machine learning practitioners to write about some of the papers and research that they found most interesting.
Here, Casey H, Machine Learning Engineer at G-Research, discusses four papers.
Fast Convex Optimization for Two-Layer ReLU Networks: Equivalent Model Classes and Cone Decompositions
Aaron Mishkin, Arda Sahiner, Mert Pilanci
Since the training objective of a neural network is typically non-convex, machine learning practitioners resort to simple iterative methods (e.g. various flavours of stochastic gradient descent (SGD)) to minimise the objective. This has the undesirable side effect that different training runs can lead to different models, sometimes with dramatically different performance.
This paper uses the fact that a two-layer feed forward network with ReLU activation function can be reformulated as a constrained convex optimisation problem. This has two major consequences:
- there are no local minima that could lead multiple training runs to converge to very different objective values
- the authors are able to bring to bear all of the sophisticated solvers for convex optimisation on the problem of training the network to convergence
The authors propose both an augmented Lagrangian and a proximal method for training the network to convergence significantly faster than the non-convex formulation using SGD. Furthermore, because the problem is convex, there are more rigourous stopping criteria to determine when the training has converged and fewer hyperparameters to tune during training (e.g. batch size, learning rate).
Transformer Quality in Linear Time
Weizhe Hua, Zihang Dai, Hanxiao Liu, Quoc V. Le
There were a number of papers this year aimed at decreasing the time and memory complexity of the self-attention mechanism at the core of many of the most recent large language models. Attention blocks are used on sequences of vectors (e.g. word embeddings for a sentence) and require time and memory quadratic in the sequence length.
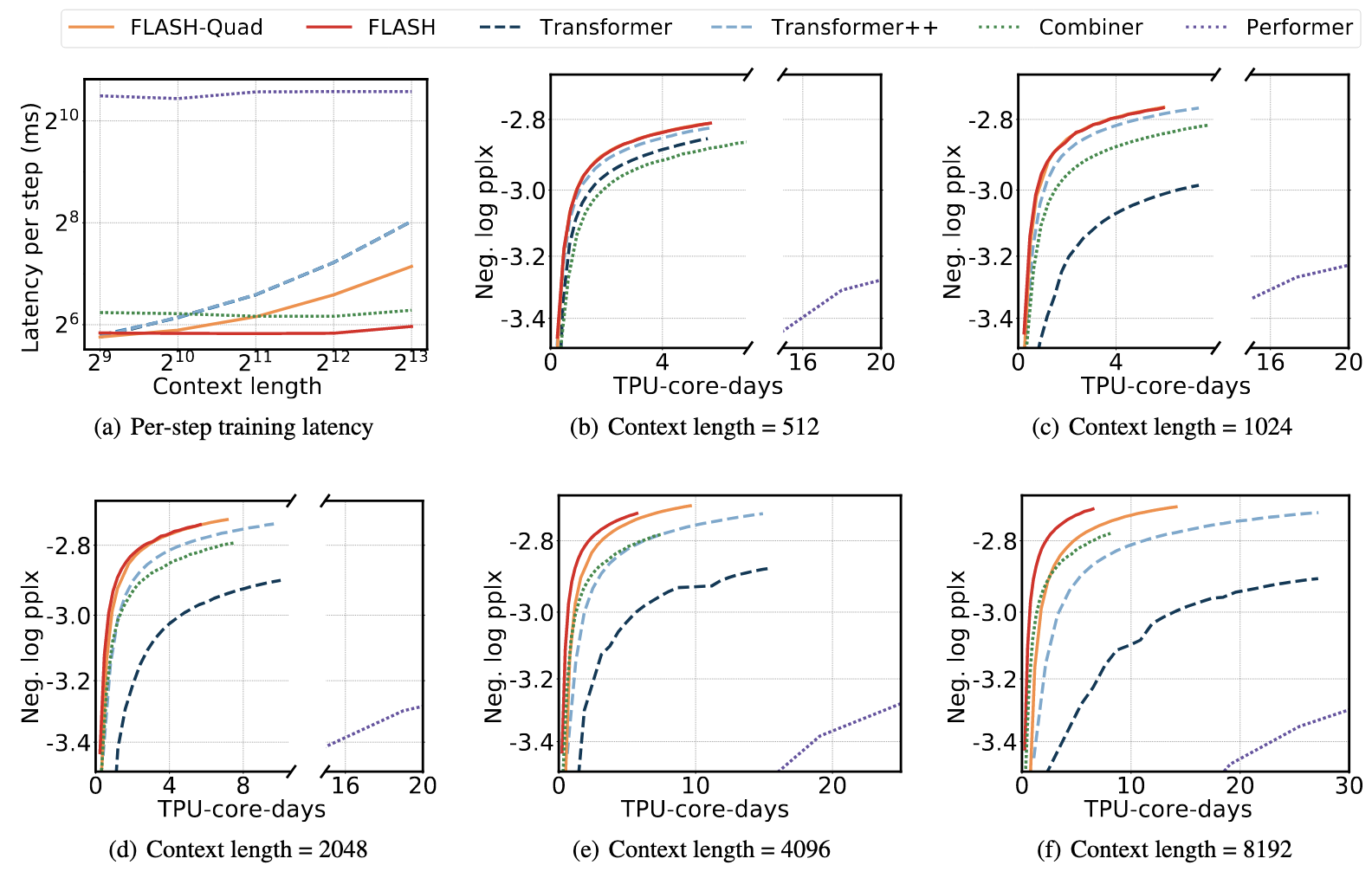
The authors of the paper propose Fast Linear Attention with a Single Head or FLASH (not to be confused with FlashAttention from Dao et al. 2022) to enable training on longer sequences without running up against GPU memory constraints.
The authors first propose a simpler version of quadratic attention, which eschews the usual row-wise softmax of the query-key matrix product for a simple elementwise activation (squared ReLU), and column-wise affine transformations of the query and key matrices. In addition, they propose a linear attention mechanism using a simple product of the query, key, and value matrices but using the associativity of matrix multiplication to do the key-value matrix product first (quadratic in the embedding dimension), thereby avoiding the query-key matrix computation (quadratic in the sequence length).
The authors then divide the sequence into disjoint chunks and apply their simpler version of quadratic attention (now quadratic in the chunk size) to each chunk separately. This is added to the global linear attention matrix they proposed in order to form a new value matrix which they use in what they refer to as a Gated Attention Unit (GAU). The GAU essentially uses the value matrix to mask a linear + activation applied to the input sequence.
This paper is interesting because it cuts against the original intuition behind attention. Attention was conceived of as a sort of “soft lookup”. Rather than look up a query in a dictionary, match it with a key and return the corresponding value, the idea behind attention was to allow the query to match with many keys and then return a weighted average of the values based on how similar the corresponding keys were with the query. This weighted average is what leads to the use of a softmax and made attention difficult to scale to larger sequence lengths.
The authors demonstrate that despite removing the nice intuitive motivations behind attention, they can still achieve comparable results in less time, using less memory.
Quant-BnB: A Scalable Branch-and-Bound Method for Optimal Decision Trees with Continuous Features
Rahul Mazumder, Xiang Meng, Haoyue Wang
Regression trees are some of the most popular methods in the machine learning community, with libraries like XGBoost and LightGBM regularly holding the top spots in Kaggle competitions. Fitting a tree to minimise the objective function exactly is usually an intractable combinatorial problem for all but the smallest datasets. As a result, all existing libraries resort to a greedy algorithm which chooses the next best split at a given node in the tree.
The authors of Quant-BnB propose a branch-and-bound method to compute the globally optimal tree of depth 2 for a continuous feature space in a more tractable time. While trees of depth 2 are useful in practice, especially in areas where interpretability is important or when there is very limited data, in many practical settings, the trees are trained to significantly deeper depths.
The key insight is to realise that any node in the tree is the root of a (sub)tree! In fact, the greedy solution is just a special case of Quant-BnB where you find the optimal tree of depth 1 with the node at the root. Instead of using the greedy algorithm at each node to grow a tree of depth 1, Quant-BnB could be used to find the best tree of depth 2 with this node at the root.
The authors note that Quant-BnB can be extended to work with deeper trees but the problem quickly becomes intractable again beyond depth 3 for even moderate data sizes.
Monarch: Expressive Structured Matrices for Efficient and Accurate Training
Tri Dao, Beidi Chen, Nimit Sohoni, Arjun Desai, Michael Poli, Jessica Grogan, Alexander Liu, Aniruddh Rao, Atri Rudra, Christopher Ré
Most of the time spent training neural networks is spent doing linear algebra computations with dense matrices such as matrix multiplication, vector addition, and solving linear equations. The authors of this paper propose replacing the dense weight matrices commonly found in neural networks with what they term “Monarch matrices”. These are essentially matrices which are block diagonal (up to a permutation), the product of which can reconstruct common transforms such as Toeplitz and Hadamard matrices.
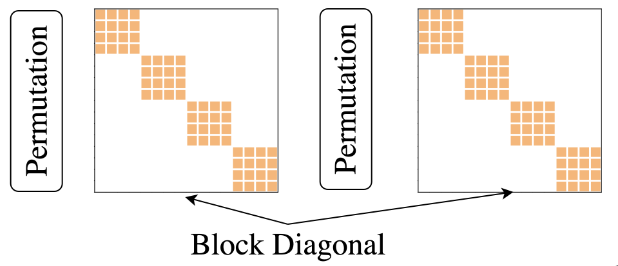
The intuition is that this low rank sparse factorisation or “Monarch parametrisation” will lead to fewer floating point operations (FLOPs). In addition, the block diagonal structure of each matrix in the parametrisation is very amenable to GPU parallelism by leveraging NVIDIA’s efficient batch matrix multiply (bmm) routines.
The authors propose three different methods for using Monarch matrices. The first is end-to-end training. A model’s dense weight matrices are simply replaced with a product of Monarch matrices and training proceeds as usual (with the 0 elements remaining frozen).
The second method is sparse to dense training where the dense weights are replaced with Monarch matrices, training proceeds until close to convergence, and then the Monarch matrices are replaced with their product and training continues with these dense matrices until convergence.
The last method is dense to sparse training in which the dense weights of a pretrained model are projected to the nearest Monarch matrix (a non-convex, yet tractable problem) and then fine-tuned using the new sparse weights.
The authors show all three of these methods can lead to a wall clock speed up time compared with traditional dense matrix training.

