Jiecheng Lu, Xu Han, Yan Sun, Viresh Pati, Yubin Kim, Siddhartha Somani, Shihao Yang
Linear attention aims to scale transformers to long sequences by reducing the quadratic cost of self-attention to O(N), but in practice often underperforms standard softmax attention, in part due to attention dilution. In causal linear attention, the output at position t is typically written as
where ϕ(·) is a kernel feature map.
This formulation enforces non-negative, sum-to-one weights, constraining outputs to the convex hull of the values.
While this convexity is benign in softmax attention, whose adaptive normalisation can become arbitrarily sharp, it becomes harmful under linearisation, hardening into a uniform averaging bias as sequence length grows.
ZeroS traces this bias to the Taylor expansion around zero of the softmax function. Writing the softmax of scores si as
where δi = si − 1/t ∑j sj, the leading term corresponds to a uniform, query-independent contribution. In exact softmax attention this term is counterbalanced by higher-order terms and adaptive normalisation, but in linear attention, where only low-order structure is retained, it dominates, driving attention toward indiscriminate averaging.
ZeroS explicitly removes this zero-order component, yielding attention weights that sum to zero before normalisation. This breaks the strict convexity constraint by allowing signed weights and contrastive interactions, while preserving the factorised structure required for efficient computation. As a result, attention can still be computed using prefix sums in linear time.
By identifying attention dilution as a consequence of the zero-order term rather than an inherent limitation of linear attention, ZeroS shows that efficient transformers can retain much of the expressive power of softmax attention without sacrificing O(N) scalability.
The results show that ZeroS closes the gap with softmax attention and performs competitively with other efficient methods such as Mamba and GLA:
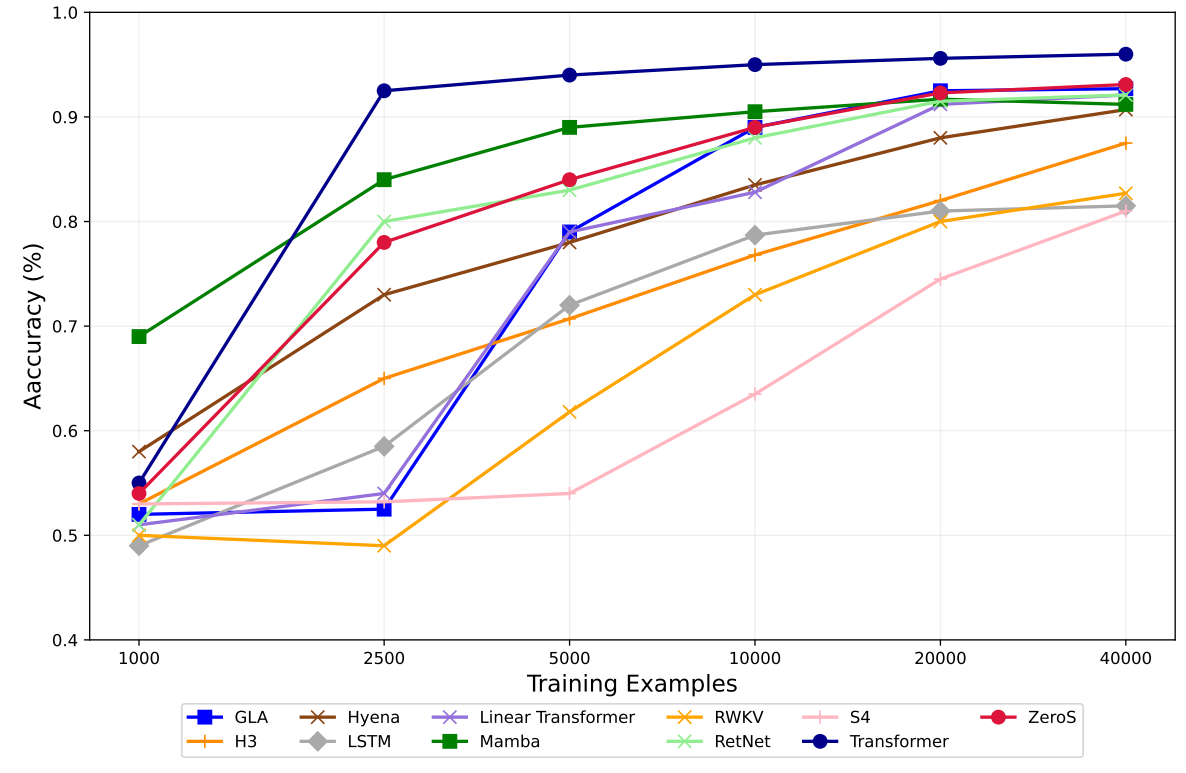
ZeroS achieves high accuracy on the RegBench benchmark suite.
ZeroS: Zero-Sum Linear Attention for Efficient Transformers