Kwangjun Ahn
This industry talk at NeurIPS presented recent research on orthonormal optimisers. These are a class of optimisation methods designed to address the scalability and conditioning issues of standard optimisers when training modern large language models (LLMs).
The motivation behind orthonormal optimisers stems from two key observations about widely used methods like AdamW:
- Memory overhead: AdamW maintains both a momentum buffer and a second-moment buffer, each roughly the size of the model itself. For LLMs with tens or hundreds of billions of parameters, these extra copies can be prohibitively expensive.
- Poorly conditioned updates: Empirically, AdamW tends to produce ill-conditioned updates. For an m×n weight matrix, many rows or columns of the update are often nearly linear combinations of others, leading to redundancy and inefficient learning.
A more recent optimiser, MUON (Momentum Orthogonalized by Newton-Schulz) addresses both issues. Unlike AdamW, which flattens matrices into long parameter vectors and applies updates independently to each element, MUON explicitly leverages the two-dimensional structure of weight matrices and enforces well-conditioned updates through orthonormalisation.
If Gt is the Nesterov momentum at step t, the update rule is:
This update rule can be derived by minimising a linear approximation of the loss function subject to a constraint that limits the update magnitude in a root-mean-square (RMS) sense.
The results on the NanoGPT speedrun benchmark show a convincing improvement over Adam:
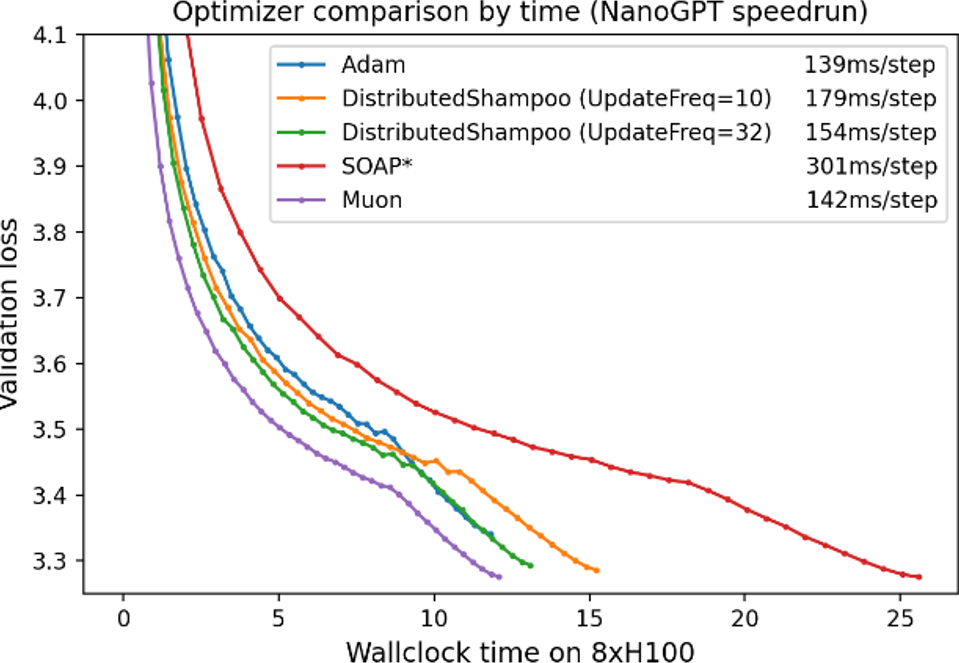
MUON improves validation loss compared to Adam for equal training time (Source: Muon: An optimizer for hidden layers in neural networks)
The primary focus of the talk was on follow-up work aimed at making MUON practical at scale. Researchers from various labs have proposed implementations and optimisations to reduce both communication overhead and redundant FLOPs, which can otherwise dominate training costs.
To this end, the talk also covered DION (Distributed Orthonormalisation) and DION-2 which retain the core idea of orthonormal updates but avoid orthogonalizing the entire weight matrix. They also replace MUON’s Newton–Schulz implementation of the Orthogonalize operation with a cheaper, iterative method that works more efficiently in distributed settings.